
来源:becominghuman.ai
作者:Jaley H Dholakiya
「机器人圈」编译:BaymaxZ
如果各位圈友对强化学习十分感兴趣,又观看过《权利的游戏》(Game of Thrones,简称GOT)的话(最好是1-7季),这个博客就太适合不过了。
强化学习!听起来很时髦,不是吗?嗯,确实是。想象一下,如果你可以教一台机器如何在一个环境中,基于奖励或惩罚来行事。就像孩子们被火烫过一次,就能学会力篝火远一点一个道理。但它实际上如何工作的呢。
简述强化学习
我们将“风暴降生”丹妮莉丝·坦格利安(Daenerys Targaryen)视为我们关注的智能体(agent),我们都知道当她说“dracary”时会发生什么(指龙母喷火)。愤怒被释放,环境亦发生变化。每次情况变化都会对丹妮莉丝或智能体造成奖励/惩罚(reward/penalty)。这提高了她的策略(policies),并且与提利昂·兰尼斯特(Tyrion Lannister)一起采取更好的动作。在愤怒之后,她转移到一个新的王国或下一个状态(state)。在了解强化学习之前,先学习这几个常用的术语,这一点很重要。
必须知道的强化学习中的术语
1.状态值函数:Vs
对于一个给定的策略和环境,它在一个状态中有多好?它可以回答约翰·斯诺(John Snow)正在徘徊的问题……哪个州/地方更有价值,临冬城或龙石岛?
2.动作值函数:Va(s)
对于给定的策略和环境,从状态s采取动作a有多好?
奖励和惩罚
在我们讨论深入的事情之前,让我们明白,什么是奖励。奖励是与达成状态有关的奖金。它就像牛仔一样,把所有的山羊从牧场赶下山就能得到奖励。这也很像在的脸书上发布文章时你大脑分泌的多巴胺。R(R(St))代表立即奖励,还有折扣奖励r(r(St)=R(St)+γ*R(S{t+1})+ gamma2 R(S_{2})...)。折扣奖励更像是你在Facebook上发布有争议的帖子时所得到的,即时奖励是好的,但未来的回报是非常负面的,最终使你重新思考发布的内容。折扣是你计算中要考虑的未来数量。γ= 1,意味着你将来会考虑一切,而γ= 0表示你根本不考虑未来,只关心立即的回报。在实际情况下,我们保持在0.9左右。
马可夫链与君临(King's landing)

我们都知道疯王(指伊里斯·坦格利安二世)的故事吧?君临(King’s Landing)是高度战斗的地方。现在,我们假设只有两个国家竞争——兰尼斯特斯(Lannisters)和史塔克(Starks)。现在假设史塔克正掌握着它。他们将来掌握它的可能性是多少?马可夫链将告诉我们答案。
看下面的代码:
import numpy as np # S: State Value of house : Its probability of retaining kings landing # P: Transition Matrix : from houseA to houseB, what is probability of transistion. houses = ["lannisters","starks"] S = {"lannisters": 0, "starks":1} P = {"from_lannisters":{"to_lannisters": 0.8, "to_starks" : 0.2 }, "from_starks": {"to_starks": 0.1, "to_lannisters": 0.9}} for i in range(5): lannisters_future_stateval, starks_future_stateval = 0,0; lannisters_future_stateval = S["lannisters"]*P["from_lannisters"]["to_lannisters"]+\ S["starks"]*P["from_starks"]["to_lannisters"]; starks_future_stateval = S["lannisters"]*P["from_lannisters"]["to_starks"]+\ S["starks"]*P["from_starks"]["to_starks"]; S["lannisters"]=lannisters_future_stateval S["starks"] = starks_future_stateval print "Voila, '%s' have been winners with %0.2f%% probability to be in king's landing "%(max(S, key=S.get),100*max(S.values()))在上面的代码中,S被初始化为[0,1],这意味着史塔克正掌握它。P代表转移概率矩阵。因此,P [“from_lannisters”] [“to_starks”]表示史塔克继承君临的概率。我们来看看君临历史上的一系列事件。
Lannisters - > Starks - > Lannisters- > Lannisters - > Lannisters - > Starks - > Lannisters - >Lannisters - >…
这个连续的继承是由过渡矩阵来模拟和解释的。我们感兴趣的是,史塔克或兰尼斯特斯的稳定状态值在君临。所以我们开始以史塔克为统治者,但把历史真理放在首位,以决定君临的命运。我们发现,兰尼斯特斯在任何时候在君临的概率都是81%。你也可以使用它来模拟你的饮食习惯。
贝尔曼最优性方程
马尔科夫过程的贝尔曼最优性方程式,我们可以把它比喻成有七个国家打仗。知道哪个王国有阴谋的最好办法就是:
·步骤1:给每个王国一个数字(初始状态值)
·步骤2:根据我对邻居王国的攻击概率(由以往记录)更新值
V(兰尼斯特斯)= p(攻击临冬城)* [攻击临冬城的即时奖励+γ*临冬城的状态值] +其他邻国也相同……
·步骤3:重复直到收敛。
我们故意留下开放式方程,因为方程式根据需要和模式不断变化。所有你需要记住的是,有一些图形评估发生在状态,以获得状态值。这个值神秘地捕捉和吸收了所有关于奖励等的判断所需要的信息。从马可夫特性直接得出,如果提供了现在的状态价值,那么它将以前的状态分解成下一个状态。
约翰•斯诺之旅的马可夫奖励流程
记得第一次当火和冰见面吗?我正在谈论的是约翰•斯诺与丹妮莉丝•坦格利安相见!其实,我们正在谈论他从龙石岛回到墙外。该部分在剧中本身非常简短。所以这里的状态是[龙石岛,白港,临冬城]。你可以通过步行去临冬城,或者你可以通过航海去白港,然后去临冬城。但是,在白港潜伏的间谍和海盗一直存在着危险。
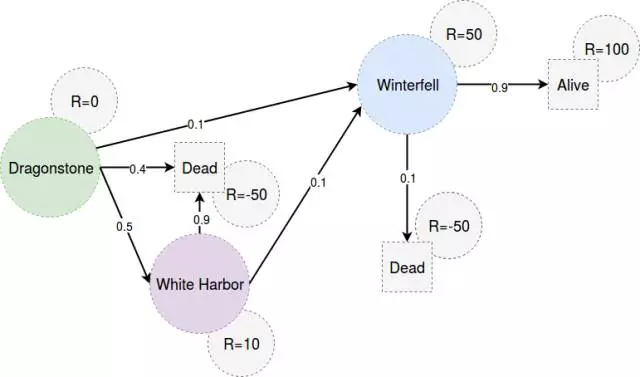
马尔科夫的奖励过程并不是什么新鲜事物,与之前的马可夫链相同,捆绑着与达成状态相关的即时奖励(在我们的案例中,它表示到达了临冬城,到达白港等)。我们计算的是,约翰·斯诺在某个特定的状态/地方有多大的奖励?换句话说,我们将计算“状态值”,它代表了在这个状态的奖励。
# Markov Reward Process Example # Finding Rewarding states for journey of John Snow from dragonstone to winterfell import numpy as np import copy S ={"dragonstone": 1,"whiteharbor":1, "winterfell":1} # Active States T=["alive-terminal","dead-terminal"] # Terminal States R = {"dragonstone": 0,"whiteharbor":10, "winterfell":50,"alive-terminal":100,"dead-terminal":-50} P ={"from_dragonstone":{"to_whiteharbor":0.5,"to_winterfell":0.1,"to_dead-terminal":0.4},\ "from_whiteharbor":{"to_winterfell":0.1,"to_dead-terminal":0.9}, "from_winterfell":{"to_alive-terminal":0.9,"to_dead-terminal":0.1}} # Probabilistic Transition Matrix gamma = 0.1 for i in range(45): S1 = copy.copy(S); for castle in S1.keys(): reward =0; from_castle='from_'+castle future_states = P[from_castle] for to_castle in future_states: reward=reward+P[from_castle][to_castle]*R[to_castle[3:]]; S1[castle] = S[castle]+ gamma*(reward-S1[castle]) S = copy.copy(S1); print S请注意,在上述马尔科夫奖励过程中,我们在任何时候没有决策我们的行为。我们只是评估给定环境的状态值(即转换矩阵,即时奖励)。该策略仅在马尔科夫决策过程的背景下形成,而不是马尔科夫奖励过程。当我们动作有自由时,决策的权利就来了。让我们来看马尔可夫决策过程。
马尔可夫决策过程——是时候动作了!
MDP和MRP在数学上是相似的,但上下文将它们分开。MDP为你提供选择。我们学习在MDP中采取特定动作的策略。可以通过以下两种方法学习MDP:值迭代、策略迭代。
在值迭代中,你不会单独学习策略。你一直在考虑从给定状态的最有益的动作作为策略,并同时使用它来更新状态值。它往往会慢一些,因为我们一次又一次地改变最佳动作(对于一个给定的状态),导致扰动。它最终会收敛,但是所花费的时间一般不会超过策略迭代。与值迭代不同,策略迭代选择策略(来自一个状态的一组动作),对其进行评估,直到收敛。一旦值收敛,我们选择一种基于值的状态稳定值的新策略,然后评估新策略。我们一直这样做,直到策略没有变化。你可以看到,这里有两个步骤:策略评估和策略更新。看看下边那个很酷的示例代码,以了解不同之处。
约翰·斯诺回家路线
约翰·斯诺打算携带MDP机器告诉他,哪个动作在某个地方/状态是最好的。他可以采取的动作一般是通过陆地、海上或龙。对于每个动作,有可能在不同的地方/状态降落。我们将会学到的是从任何状态/地方选择的最佳策略。代码可以自解释,所以你可以在jupyter上运行这个代码,自己就知道是怎么回事了。我假设你们都安装了numpy,这听起来很合理。
值迭代
# Markov Decision Process Example import numpy as np import copy S ={"dragonstone": 1,"whiteharbor":1, "winterfell":1} # Active States T=["alive-terminal","dead-terminal"] # Terminal States R = {"dragonstone": 0,"whiteharbor":10, "winterfell":50,"alive-terminal":100,"dead-terminal":-50} P ={"from_dragonstone":{"land":{"to_winterfell":0.5,"to_dead-terminal":0.5},\ "sea":{"to_whiteharbor":0.1,"to_dead-terminal":0.9},\ "dragon":{"to_winterfell":0.95,"to_dead-terminal":0.05}},\ "from_whiteharbor":{"land":{"to_winterfell":0.6,"to_dead-terminal":0.4}}, "from_winterfell":{"land":{"to_alive-terminal":0.9,"to_dead-terminal":0.1}}} gamma = 0.1 A ={"from_dragonstone":{"land":1,\ "sea":1,\ "dragon":1}, "from_whiteharbor":{"land":1}, "from_winterfell":{"land":1}} Policy = {"from_dragonstone":"land","from_whiteharbor":"land","from_winterfell":"land"} # Solution by Value Iteration for i in range(15): S1 = copy.copy(S); for castle in S1.keys(): from_castle='from_'+castle future_states = P[from_castle] action_reward={} for action in A[from_castle]: reward =0; for to_castle in future_states[action]: reward=reward+P[from_castle][action][to_castle]*R[to_castle[3:]]; action_reward[action]=reward Policy[from_castle]=max(action_reward,key=action_reward.get) S1[castle] = S[castle]+ gamma*(max(action_reward.values())-S1[castle]) S = copy.copy(S1); print 'Value Function',S print 'Learned Policy',Policy策略迭代
# Markov Decision Process Example import numpy as np import copy S ={"dragonstone": 1,"whiteharbor":1, "winterfell":1} # Active States T=["alive-terminal","dead-terminal"] # Terminal States R = {"dragonstone": 0,"whiteharbor":10, "winterfell":50,"alive-terminal":100,"dead-terminal":-50} P ={"from_dragonstone":{"land":{"to_winterfell":0.5,"to_dead-terminal":0.5},\ "sea":{"to_whiteharbor":0.1,"to_dead-terminal":0.9},\ "dragon":{"to_winterfell":0.95,"to_dead-terminal":0.05}},\ "from_whiteharbor":{"land":{"to_winterfell":0.6,"to_dead-terminal":0.4}}, "from_winterfell":{"land":{"to_alive-terminal":0.9,"to_dead-terminal":0.1}}} gamma = 0.1 A ={"from_dragonstone":{"land":1,\ "sea":1,\ "dragon":1}, "from_whiteharbor":{"land":1}, "from_winterfell":{"land":1}} Policy = {"from_dragonstone":"land","from_whiteharbor":"land","from_winterfell":"land"} #Solution by Policy Iteration Policy = {"from_dragonstone":"land","from_whiteharbor":"land","from_winterfell":"land"} for i in range(50): S1 = copy.copy(S); #Step 1 : Update Value Fuction for castle in S1.keys(): from_castle='from_'+castle future_states = P[from_castle] action = Policy[from_castle] #Based on policy for to_castle in future_states[action]: reward=reward+P[from_castle][action][to_castle]*R[to_castle[3:]]; action_reward[action]=reward S1[castle] = S[castle]+ gamma*(reward-S1[castle]) S = copy.copy(S1); #Step 2 : Update Policy for castle in S1.keys(): from_castle='from_'+castle future_states = P[from_castle] action_reward={} for action in A[from_castle]: reward =0; for to_castle in future_states[action]: reward=reward+P[from_castle][action][to_castle]*R[to_castle[3:]]; action_reward[action]=reward Policy[from_castle]=max(action_reward,key=action_reward.get) #Update Policy print 'Value Function',S print 'Learned Policy',Policy返回搜狐,查看更多
责任编辑:

